Tetration

Tetration is repeated exponentiation. We can define ⁰b = 1, ¹b = b, ²b = b^b, ³b = b^b?, etc. In fact,

{\hskip 30pt ^{n}b}=\underbrace {b^{b^{\cdot ^{\cdot ^{b}}}}} _{n}.

We can recursively define tetration for the base b with F(0) = 1, F(x + 1) = b^x. Working backwards from this definition, we see that F(−1) = 0, and F(−2) is undefined. The big question is whether we can extend the function F(z) to the whole complex plane, except for a branch cut z < −2. Dr. Paulsen, along with Samuel Cowgill, has proven that in fact there is a unique way to create the function F(z), such that the limit of F(z) as the imaginary part of z goes to +∞ tends to the complex fixed point of the exponential function b^z. The details are in the paper "Solving F(z + 1) = b^F(z) in the complex plane". The paper has been published in "Advances in Computational Mathematics". The online version can be found at http://rdcu.be/pROI. The follow-up paper in the same journal, "Tetration for Complex Bases" can be found at http://link.springer.com/article/10.1007/s10444-018-9615-7.

The authors also devised a quick way of computing F(z) to 50 places of accuracy. From this, they could have Mathematica draw complex contour maps of the function F(z).

In fact, Dr. Paulsen has written an interactive tetration calculator that computes 20 places of accuracy in javascript. This tetration calculator can be found here.

For example, here is the contour map for the base b = 2:

Here is the contour map for the base b = e, sometimes known as the natural tetration.

Some of the prominant features of this graph are the "pineapple top" at 2.5, the "ears" at 4 ± 0.75 i, and the "wagonwheels" at 7.5 ± 0.5 i.

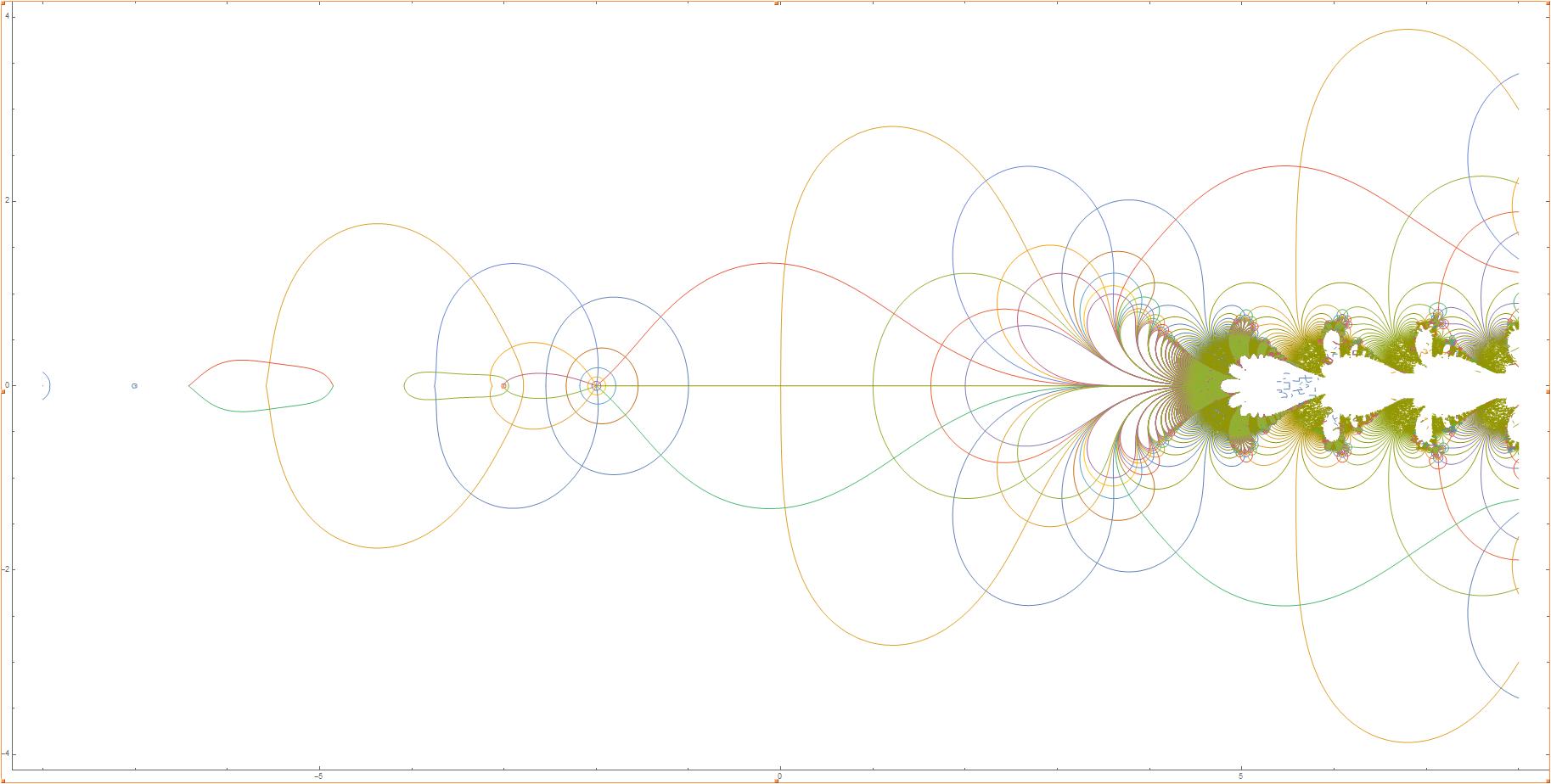
Finally, here is the contour map for the base b = 10, known as the common tetration. It took several days for Mathematica to draw this.

The "ears" and "wagonwheels" are still present (but moved), but not there are several other interesting features. We begin to see a repeating pattern along a diagonal line, because of a complex psuedo-period.

In a second paper, "Tetration for Complex Bases", Dr. Paulsen was able to analytically extend the tetration to complex values of b. For example, here is the contour map for the base b = 3 + i:

The graph is already looking asymetrical. As the base moves to b = 2 + i, the parts start to separate.

Here is the contour plot for b = 1 + i:

Notice that now, there are "spontaneous branch cuts" on the upper left hand side of the graph. We can even go all the way to b = i:

One base of particular interest is the Sheldon base, b = 1.525982338517 + 0.0178411853321 i.

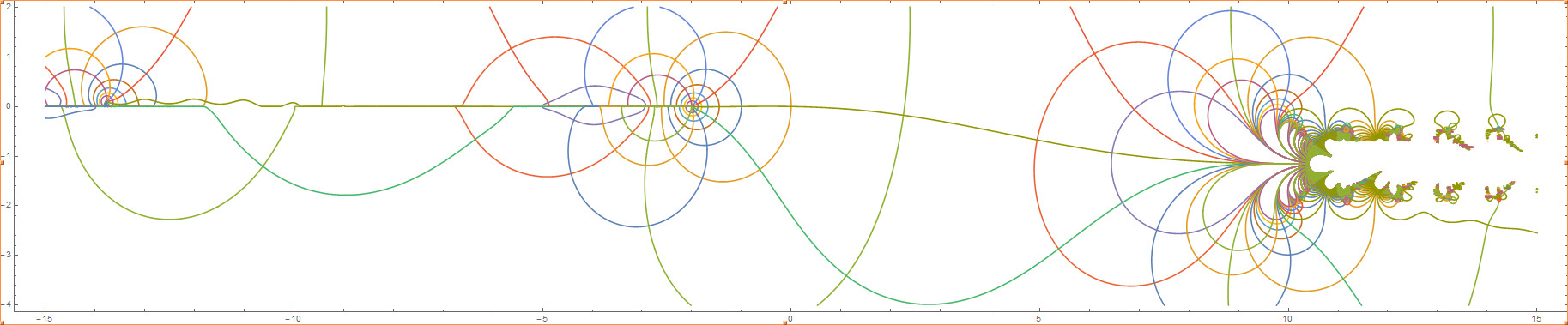
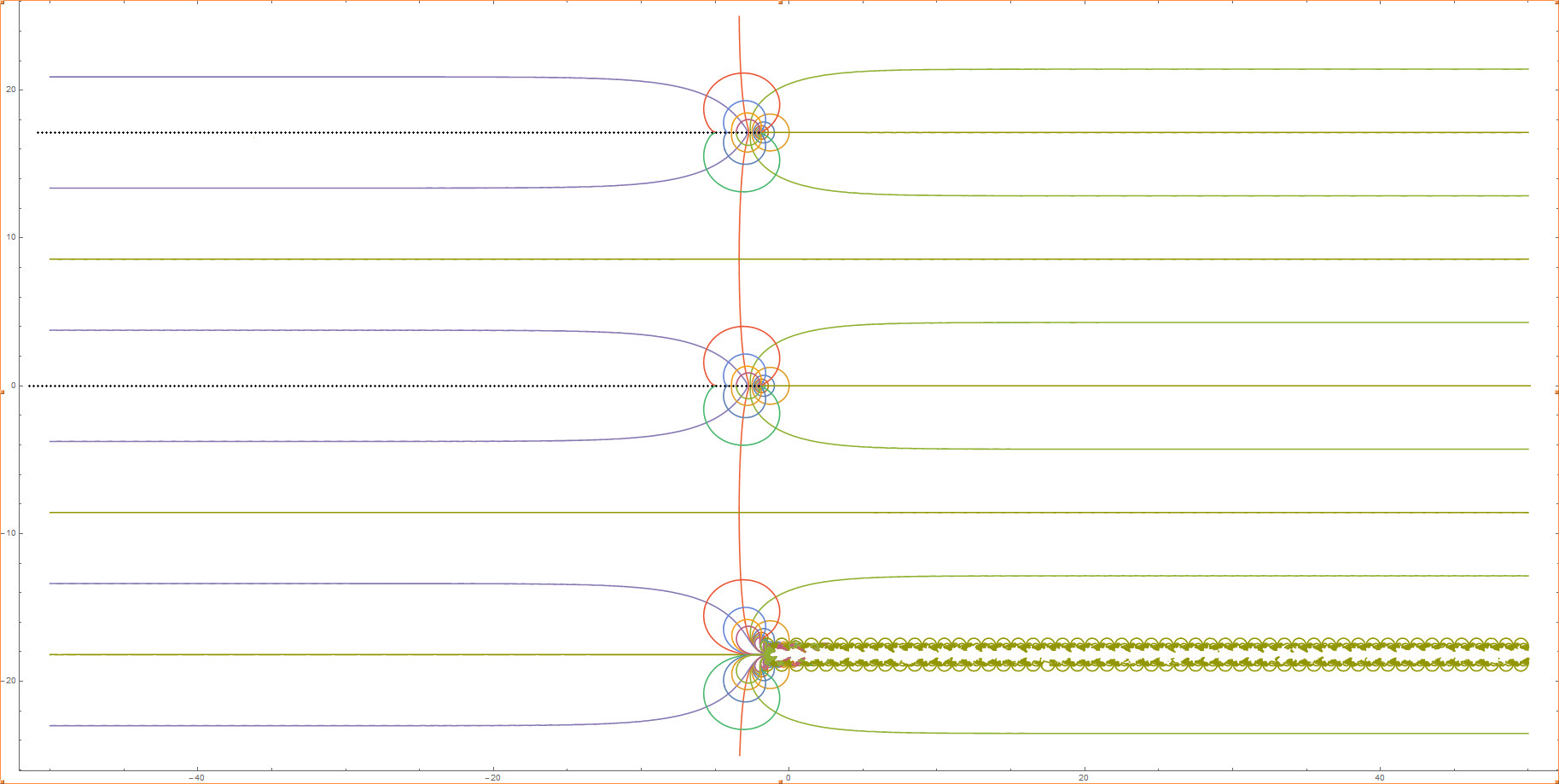
And now for something very surprising. If we analytically continue the complex tetration back onto the real number line, between 1 and e^1/e, we do not quite get a symmetric function! Here is what we get when we approach b = √2 from above the real axis.

The Mathematica notebooks, CrossTrack.nb and DaggerTrack.nb, that construct the F(z) function for real and complex bases, as well as the commands that were used to create these pictures, can be downloaded here.